martes, 5 de mayo de 2015
Notación de conjuntos
Historia
Los Griegos tomaron elementos de la matemática de los Babilonios y de los Egipcios. La innovación más importante fue la invención de las matemáticas abstractas basadas en una estructura lógica de definiciones, axiomas y demostraciones. Según los cronistas griegos, este avance comenzó en el siglo VI a.c. con Tales de Mileto y Pitágoras de Samos. Este último enseñó la importancia del estudio de los números para poder entender el mundo. Algunos de sus discípulos hicieron importantes descubrimientos sobre la teoría de números y la geometría, que se atribuyen al propio Pitágoras.
Las ideas conjuntistas tienen vigencia en todas las actividades del hombre
y constituyen un elemento básico
del pensamiento racional. Todos
los sistemas matemáticos utilizan el lenguaje de la teoría de conjuntos para expresar
las propiedades, relaciones y operaciones entre los elementos que hacen parte de cada sistema matemático.
Podemos decir que
un conjunto es una colección de objetos de una misma naturaleza que
cumplen una propiedad determinada. Los objetos de un
conjunto reciben el nombre de ELEMENTOS y se representan por letras
minúsculas o por números.
Los conjuntos se
simbolizan por letras mayúsculas y
sus elementos se encierran entre llaves o corchetes, separándolos con una coma.
Ejemplos
1.
Los objetos que están en el salón de
clase
2.
Los alumnos del colegio
3.
Los profesores del colegio
4.
Las vocales
5.
Los países de Suramérica
Los conjuntos
también se pueden representar gráficamente por medio de figuras geométricas como círculos, rectángulos, cuadrados
o curvas cerradas,
esta representación la llamaremos DIAGRAMAS
DE VENN,
ya que éste matemático fue quién
utilizó esta forma para representar los
conjuntos.
Ejemplos
Sean los
siguientes conjuntos:
1. Sea A el conjunto de los dígitos
2.
Sea B las vocales abiertas
3. Sea C las vocales cerradas
Pertenencia y no
pertenencia
Cuando decimos
que un conjunto está constituido por elementos, establecemos una relación entre un elemento y el conjunto, ésta relación la llamaremos relación de pertenencia.
Dados un elemento a y un conjunto A, puede ocurrir uno de los siguientes eventos:
El cardinal de un conjunto es el número natural que representa la cantidad de elementos que
contiene el conjunto y se denota por: # (
A) = n ¨ El número de elementos de A es n ¨
Si miramos el ejemplo anterior, podemos decir que el cardinal del conjunto B
estará dado por:
#(
B) = 5 porque el conjunto B tiene 5 elementos.
Determinación
de conjuntos
Los elementos que pertenecen a un
conjunto se pueden nombrar de dos
formas: por extensión o por
comprensión.
Extensión
Un conjunto cualquiera se determina
por extensión
cuando se nombra a cada uno de sus elementos. Por ejemplo:
El
conjunto C
representa a las vocales
Comprensión
Un conjunto cualquiera se determina
por comprensión cuando se le da una propiedad común a todos sus
elementos. Utilizaremos la notación:
{X / X} Que se lee:
¨ El
conjunto de las X, tales que X ¨ Por ejemplo:
El conjunto C se lee: ¨ El conjunto de las X, tales que X es una vocal ¨ 
Cuando se conoce el número de elementos de un conjunto, éste se llamará
conjunto FINITO, por lo tanto su cardinal es
n. Si el número de elementos no se
puede determinar, el conjunto será INFINITO, es decir que no existe un
número natural que represente su cardinal.
lunes, 4 de mayo de 2015
Tipos de conjuntos
Los conjuntos
pueden ser: universal, unitario o vacío.
Conjunto
universal
Es aquel que está formado por todos
los elementos de una misma especie y que sirve como referencia para definir a
otros conjuntos, también se llama conjunto
referencial y se representa por la letra
U.
Sea U = {X /
X es un número dígito}
Se puede observar
en el conjunto anterior que U está formado por los dígitos pares, los dígitos
impares, y por el cero, por lo tanto el
conjunto universal U contiene a otros conjuntos,
es decir:
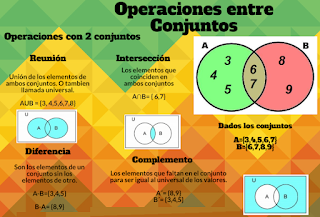
Operaciones entre conjuntos
Las principales operaciones entre
conjuntos son: unión, intersección, diferencia y complemento.
Unión
entre conjuntos
La unión de los conjuntos A y B es el conjunto formado por todos los
elementos que pertenecen al
conjunto A o al conjunto
B o a ambos. La unión se denota por A U B y simbólicamente estará dada por:
Sistemas lógicos
Todas las ciencias están basadas en
principios filosóficos. La matemática se basa en los principios de la lógica
matemática, que ayuda a resolver
muchos por qués y contribuye a clarificar
las demostraciones de los razonamientos.
Una proposición es una frase o
expresión con sentido lógico de la cual se puede decir que es verdadera o falsa. La verdad o falsedad
de una proposición se llamará valor
de verdad. Las proposiciones se representarán con
letras minúsculas como: p, q, r ,s, t, u, v, ……. Por ejemplo:
p: 2 es un número
par. Verdadera
q: La capital de
Colombia es Medellín. Falsa
r: Los pájaros
vuelan. Verdadera
s: 3 + 5 = 9 Falsa
Las frases interrogativas, afirmativas o
desiderativas son expresiones que no tienen sentido lógico, por lo tanto no se
le puede asignar un valor de verdad y no se considerarán proposiciones,
ya que no se conoce sujeto alguno. Por ejemplo:
¿Es verdad?
Llueve
Amanecerá y
veremos ¿Está lloviendo?
Las proposiciones son expresiones que constan de un sujeto lógico o término y de un predicado,
por lo tanto pueden ser cerradas o abiertas.
Proposiciones cerradas
Son aquellas proposiciones de las
cuales se puede decir que son verdaderas o falsas, ya que se conoce su sujeto lógico. Por ejemplo:
p: 3 es un número
par. Verdadera
q: Medellín es la
capital de Antioquia. Verdadera
r:
Los pájaros nadan. Falsa
s: 3 + 5 = 9 Falsa
Proposiciones
abiertas
Son aquellas proposiciones de las
cuales no se puede decir que son verdaderas o falsas, ya que no se conoce su sujeto lógico. Por ejemplo:
t: X es un número
par.
u: Y es la capital
de Antioquia.
v: Z es un dígito
natural.
s: X
- 5
= 10
Una proposición abierta se puede
convertir en cerrada cuando el sujeto
lógico o término se reemplaza
por un término constante.
t: X es un número
par. Proposición abierta
t: 4 es un número
par. Proposición
cerrada
u: Y es la capital
de Antioquia. Proposición abierta
u: Cali es la capital de Antioquia. Proposición
cerrada
Tipos de proposiciones
Las proposiciones se clasifican
en proposiciones simples y proposiciones
compuestas
Proposiciones simples
Son
todas aquellas proposiciones cerradas de las cuales se dice una sola
idea, es decir que solo hay un predicado.
Por ejemplo:
p: 0 es un dígito natural. Verdadera
q: Colombia es un país suramericano. Verdadera
r: La tierra es
un satélite. Falsa
s: 3 + 2 es igual a
5. Falsa
Proposiciones compuestas
Una proposición compuesta es aquella
que está formada por dos o más
proposiciones simples relacionadas
por medio de conectivos lógicos.
En otras palabras son todas aquellas proposiciones cerradas en las cuales hay
dos o más ideas. Por ejemplo:
p: La tierra es un
planeta y es hermosa.
q: La luna es un
satélite o es un planeta.
Ejemplo
Sean las proposiciones:
p:
0 es un dígito natural.
q:
Colombia es un país suramericano.
r: La tierra es
un satélite.
s: 3 + 2 es igual a 5.
p ^ s:
0 es un dígito natural y 3+2 es igual a 5
q
V r: Colombia es un país suramericano o la tierra es un satélite
Suscribirse a:
Entradas (Atom)